频域稳定判据

利用开环频率特性判断闭环系统的稳定性

幅角原理

在复平面 $[s]$ 任取一条闭合曲线 $\mathrm{\Gamma }$，包围 $F(s)$ 的 $Z$ 个零点和 $P$ 个极点，且不通过 $F(s)$ 的任何零点和极点
当复变量 $s$ 沿曲线 $\mathrm{\Gamma }$ 顺时针绕一周时，在平面 $[F]$ 上，${\mathrm{\Gamma }}_F$ 包围原点的圈数 $R=P-Z$

开环传递函数 ： $G(s)H(s)$
1+开环传递函数： $F(s)=1+G(s)H(s)$

也即：闭环传递函数的分母
$F(s)$ 的根，即 $F(s)$ 的零点，为闭环传递函数的极点

• $Z$ 为 $F(s)$ 的零点个数，也即闭环传递函数的极点个数
• $P$ 为 $F(s)$ 的极点个数，也即开环传递函数 $G(s)H(s)$ 的极点个数
• $R$ 为 $F$ 对应的曲线 ${\mathrm{\Gamma }}_F$ 包围原点的圈数，也即开环传递函数包围 $(-1,j0)$ 的圈数

系统稳定的充分必要条件为：闭环系统特征方程的所有根均具有负实部

所以我们重点讨论右半平面

选择闭合曲线 $\mathrm{\Gamma }$ 包围复平面的右半平面和虚轴，若被包围的 $F(s)$ 零点数 $Z=0$，则闭环系统稳定，因为 $Z=P-R$，开环传递函数在右半平面的极点个数为 $P$

所以判断系统的稳定转化为判断 $F(s)$ 右半平面包围的零点个数，转化为求 $F(s)$ 包围零点的圈数 $R$，即求开环传递函数包围 $(-1,j0)$ 点的圈数 $R$

Nyquist 判据

对于增补后的 Nyquist图

闭环系统稳定的充要条件：曲线 ${\mathrm{\Gamma }}_{GH}$ 不穿过 $(-1,j0)$, 且逆时针包围 $(-1,j0)$ 的圈数 $R$ 等于开环传递函数正实部极点的个数 $P$

正负穿越法：$\omega :0\to +\mathrm{\infty }$ ，${\mathrm{\Gamma }}_{GH}$ 穿越 $(-1,j0)$ 左侧负实轴的次数

逆时针为正方向

• 正穿越 $N^{+}$：从上到下，辐角逐渐增大，穿越左侧负实轴
• 负穿越 $N^{-}$：从下到上，辐角逐渐减小，穿越左侧负实轴(增补的穿越都为负穿越)
• 半次正穿越 ${\displaystyle \frac{1}{2}}{N}^{+}$ 起于负实轴
• 半次负穿越 ${\displaystyle \frac{1}{2}}{N}^{-}$，终于负实轴

逆时针包围的圈数 $R$ ：

Bode 判据

对于增补后的 Bode 图

Nyquist 图中：${\mathrm{\Gamma }}_{GH}$ 穿越 $(-1,j0)$ 左侧负实轴的次数，对应 Bode 图中：幅频特性大于 $0dB$ 的所有频率内，相频特性穿越 $(2k+1)\pi$ 的次数

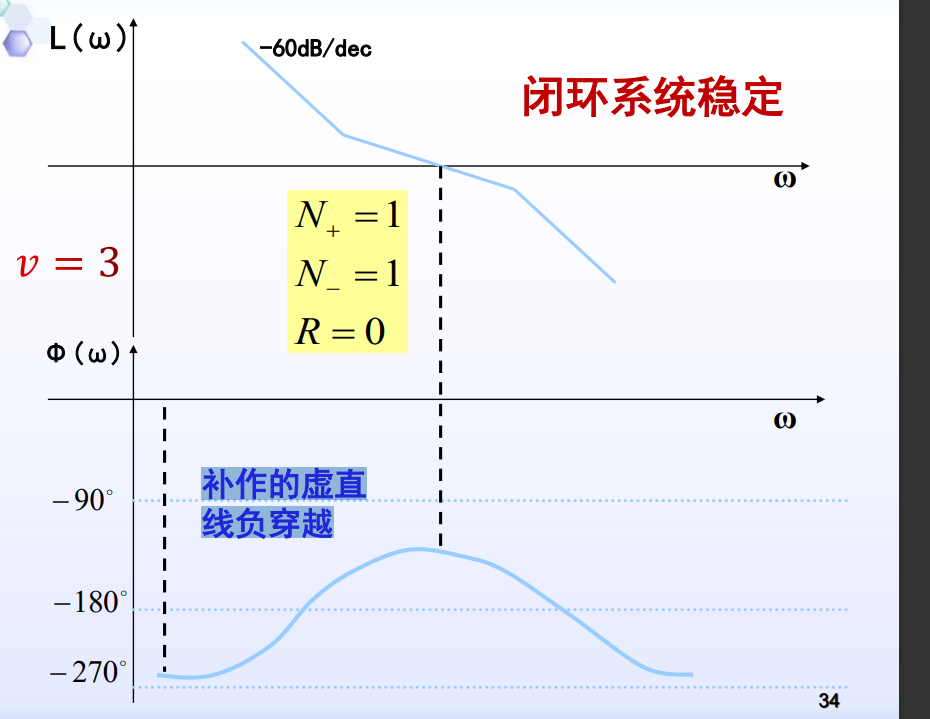
补作的虚直线都为负穿越：